【以太坊源码分析】IV. 椭圆曲线密码学与椭圆曲线数字签名算法在以太坊中的应用

数字签名算法在以太坊中有很多应用，目前已知的至少有两种：一种是在每笔交易（Transaction, tx）对象产生时对整个tx对象进行数字签名； 另一种是在共识算法中的Clique算法实现中，新创建的块在Seal()函数中被数字签名，该函数对新块进行授权/封存。 这两个地方使用的签名算法是椭圆曲线数字签名算法（ECDSA）。 在使用ECDSA进行数字签名的基础上，基于自身业务需求，以太坊将数字签名过程中使用的公钥作为地址类型（common.）使用。

关于ECDSA的几个理论概念之间的关系如下： 椭圆曲线数字加密算法ECDSA是数字签名算法（DSA）的变种之一，ECDSA的基础是椭圆曲线密码学（Elliptic-curve cryptography，ECC），而ECC的理论前提是椭圆曲线上的点相乘（Elliptic curve point multiplication）。 本文将从这些概念的原理入手，尝试解释以太坊采用的ECDSA的来龙去脉。

1.椭圆曲线点乘积的概念知识

椭圆曲线的点乘是指椭圆曲线上的一个点沿着曲线不断地与自身相加，最后落在曲线上的另一个点上的（计算）过程。 可能有些地方会把这里的乘法翻译成“积”或者“乘法”。 在这种情况下，应特别注意。 这个所谓的“点积”特指一个标量和一个点的乘积，属于标量乘法（scalar multiplication）。 因此，个人认为这里的point multiplication翻译成“point multiplication”会更准确，本文将沿用这个翻译。

假设起点为椭圆曲线上的P点，终点为曲线上的R点，则有如下点积公式。 注意此时标量一定要写在点的左边。

R = nP

上式中的结果R点还不能计算出来，需要更多的准备工作。 理论上，这里椭圆曲线选择的几何方程是固定的，可以表示为：

y^2 = x^3 + 轴 + b

上式中，a、b为普通标量参数。 上式绘制的几何曲线如下图所示，其中红色曲线表示(a, b) = (-7, 6)时的椭圆曲线，蓝色曲线表示(a, b)时的椭圆曲线= (-6, 6)。 显然，a和b的取值对曲线的形状还是有影响的。

既然我们有了椭圆曲线的具体形状和方程，假设曲线上有一个点P，我们要计算它的乘积nP，应该怎么做呢？

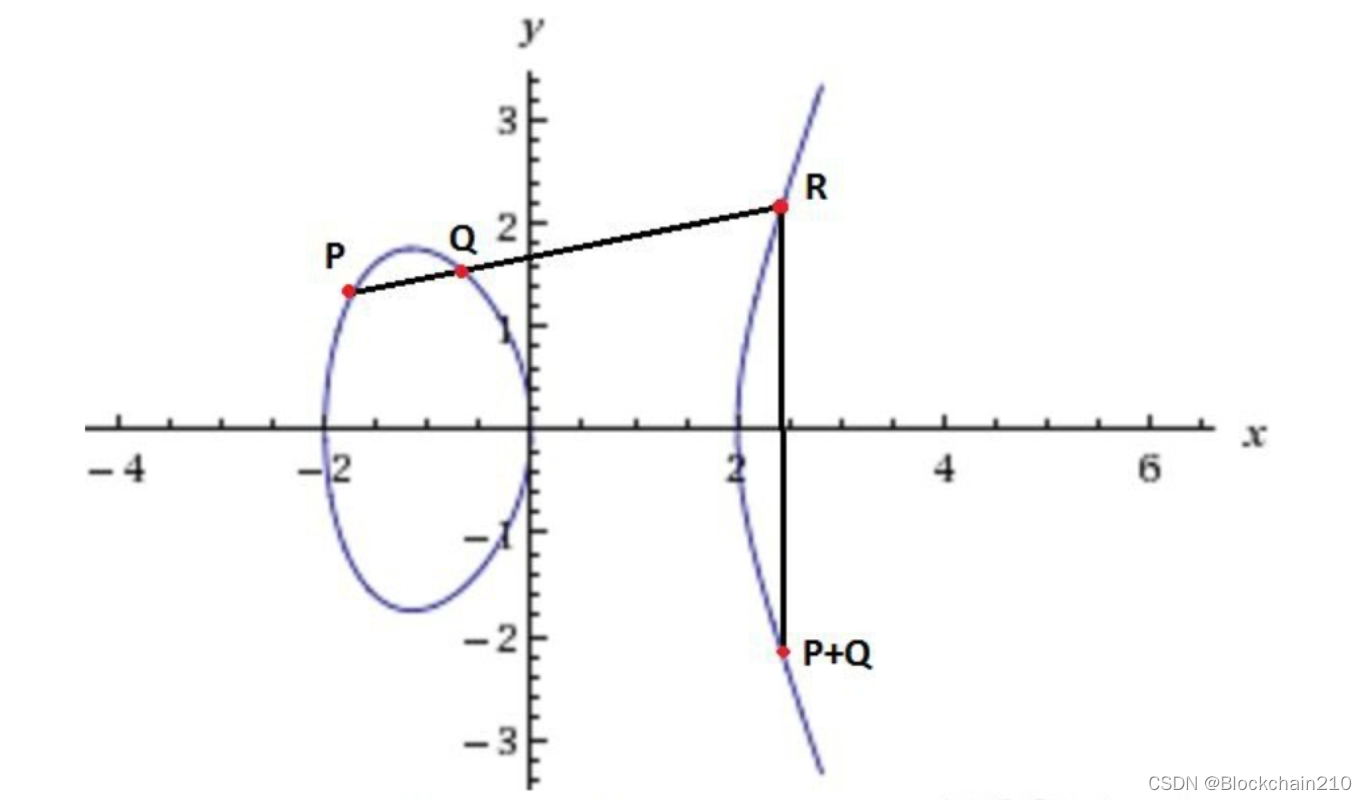
这里需要引入另一个概念：椭圆曲线点的点加法。 以上图为例。 红色椭圆曲线上有两个点P和Q。 将这两个点相加得到一个也在曲线上的点R。 这个点R来自P和Q，它们直接连接到延长线和椭圆。 曲线交点（T点）的共轭点，即T点沿X轴的对称点R。 由于上述椭圆曲线本身必须沿X轴对称，因此该点R也必须在曲线上。

让我们从代数的角度重新审视这个问题：

这里我们用XY坐标表示P,Q,R的各个点，结合设定的椭圆曲线公式y^2 = x^3 + ax + b，可以得到如下答案：

通过引入一个参数lambda，我们可以通过将P和Q两点相加得到R点的坐标。

很好，让我们再往前走一步。 如果P点和Q点重合，将它们加到R点呢？ 这种情况称为椭圆曲线点的加倍或叠加（point double）。 根据上式，R点的x、y的相对坐标不变。 我们只需要使用一个特殊的lambda值即可，但要注意此时的lambda值与曲线方程的参数a有关：

好了，有了上面的基础，我们终于可以计算椭圆曲线上点的倍数了，因为对于R = nP，不管n取什么值，我们都可以用“乘”的方法计算出R点的坐标。

计算方法

下面来看看如何计算椭圆曲线点乘积Q = dP，即已知椭圆曲线点P和标量d，计算出曲线点Q。

在开始写代码之前，标量d需要用二进制表示，这样才能应用“加点”和“加倍”的方法。

上式是d的二进制表示。 代码中，每个系数可以表示为一个长度为(m+1)的数组d[]，d[i]对应第i位的值0或1。 以下伪代码来自 wiki-PointMultiplication。

最直观的就是迭代，比如自下而上的迭代：

[清楚的]

//迭代：索引递增 N=P;Q=0; foriin[0,m]do: ifd[i]==1thenQ=point_add(Q,N) N=point_double(N) returnQ

还有从上到下的迭代：

[清楚的]

//迭代：indexdecreasing Q=0; foriin[m,0]do: Q=point_double(Q) ifd[i]==1thenQ=point_add(Q,P) returnQ

可以看出，自顶向下迭代算法的计算量与前者完全相同，但可以少用一个局部变量N。

除了迭代，当然还有递归

[清楚的]

//递归 funcf(p,n) is ifn==0then return0 elseifn==1then returnp elseifnmod(2)==1then returnpoint_add(p,f(p,n-1)) else returnf(point_double(p),n/ 2)

此外，它还可以针对窗口宽度进行优化。 注意d之前是用二进制表示的，窗口宽度可以表示为1，即每次的2+1次方。如果现在选择更合适的窗口宽度w，d可以表示为

这样得到的m更小，即系数数组d[]的长度更小，意味着只需要更少的迭代（递归）次数。 有关伪代码，请参阅 wiki。

2. 椭圆曲线密码学

椭圆曲线密码学（Elliptic curve cryptography，简称ECC）和目前流行的其他几种密码学一样，也是使用一对由公钥+私钥组成的密钥来进行加密相关的操作。 它基于有限域上的特定椭圆曲线运行。 最重要的操作是椭圆曲线的点积。 毫不夸张地说，椭圆曲线的点积是椭圆曲线密码学的基石。

你为什么这么说？ 因为对于点积Q=nP的计算公式，在已知起点P和终点Q的情况下，在目前的计算条件下理论上几乎不可能计算出n！ 这个数学证明过程比较复杂，这里只想举一个极端的例子。 回头看上一章的图，如果这里选择图中的红色椭圆曲线进行点积运算，注意它的左边部分是闭合的不规则圆弧，如果积运算的终点Q发生落在这个圆弧上，生死不能计算参数n，因为如果n增加，那么在圆弧上再绕几圈Q就会一直停留在Q点...

加密椭圆曲线参数集

ECC的使用场景包括数字签名、安全伪随机数生成等。在应用中，使用的椭圆曲线必须定义一套完整的参数，称为域参数。一般来说，ECC定义的参数集可以是表示为

(p, a, b, g, n, h)

其中，p是一个很大的质数，用来表示曲线上所有点的范围； a和b分别是椭圆曲线方程y^2 = x^3 + ax + b中的系数； G是椭圆曲线上的点积 对于点积运算得到的曲线上点的集合，G可以看成是它们的生成器（generator）； n为基点G的可乘阶数，定义为能够使点积nG不存在的最小整数n； h为整型常量，与椭圆曲线运算得到的点集和n有关，h一般取1。

在下一节中，我们可以看到这些椭圆曲线参数在椭圆曲线数字签名中的应用。

3. 椭圆曲线数字签名算法理论

椭圆曲线数字签名算法（ECDSA）是数字签名算法（DSA）的变体之一，它基于椭圆曲线密码学。 与基于RSA密码学的DSA相比，ECDSA计算数字签名所需的公钥长度可以大大缩短。 例如，对于安全级别为80位的数字签名，ECDSA要求的公钥长度仅为安全级别的两倍，即160位，而RSA在相同安全级别要求下要求的公钥长度为至少 1024 位； 同时算法生成的签名长度，无论是ECDSA还是RSA，都在320位左右。 这样，ECDSA在应用上相对于RSA的优势就很明显了。

注意：安全级别的概念是：N位的安全级别，也就是说攻击者需要大约2^N次操作才能得到本次加密所用的私钥。 安全级别所代表的比特位越长，安全性能越好，越难破解。 当然，加密的成本，包括公钥的长度和生成的签名的长度，自然会相应增加。

ECDSA基于DSA，定义了数字签名生成过程和验证过程的基本步骤。 通过对比可以看出，ECDSA遵循了DSA的这些定义，在一些具体的步骤中，使用了椭圆曲线的相关操作。 由于篇幅有限，这里就不详细介绍DSA的内容了。 有兴趣的朋友可以去wiki看看。

数字签名的生成

下面我们来看一下ECDSA的签名生成过程。 以下内容主要来自wiki_ECDSA

假设 Alice 要向 Bob 发送经过数字签名的消息，他们首先需要为椭圆曲线加密定义一组普遍接受的参数。 简单地说，这组参数可以表示为

（曲线，G，n）

其中，CURVE表示椭圆曲线点场和几何方程； G是所有加倍操作的基点； n是椭圆曲线的乘法阶数，作为一个大素数，n的几何意义在于，nG = 0，即点积nG的结果不存在，对于任意正整数m = [ 1，n-1]小于n，点积mG可以得到合理的椭圆曲线点。

其次，爱丽丝创建一对密钥，一个私钥和一个公钥。 私钥来自[1, n-1]范围内的随机数：

公钥如下，由私钥与基点的椭圆曲线点积导出：

好了，准备工作就绪，假设Alice要对消息m进行数字签名，有以下步骤：

计算e = HASH(m)，HASH是哈希加密函数，如SHA-2，或SHA-3。 计算z，从e的二进制形式的最左边（即最高）L_n位开始计算，L_n为上述椭圆曲线参数中乘法阶数n的二进制长度。 请注意，z 可能大于 n，但它的长度永远不会长于 n。 从[1,n-1]中随机选择一个满足密码随机安全的整数k。 计算椭圆曲线上的一个点： 计算r值用下面的公式，如果r == 0，返回步骤3重新计算。 用以下公式计算s的值，如果s == 0，则返回步骤3重新计算。 生成的数字签名为(r, s)

需要特别注意步骤3中k的选择，它既要满足密码学的随机安全要求，又要像私钥一样受到保护。 更重要的是，每次产生新的数字签名时，这个k都必须每次更新。 否则，很容易通过上述数字签名过程中计算公式的相互转换来破译私钥！ 具体转换过程可以参考wiki_ECDSA。

数字签名的验证

对于消息的接收者 Bob 来说，除了收到数字签名文件外，他还将拥有一个公钥。 所以Bob的验证分为两部分，先验证公钥，再验证签名文件(r,s)。

公钥验证

公钥

坐标应有效且不会等于极限值零点

通过公钥

它必须是椭圆曲线上的一个点。

下式应成立，即曲线的乘法阶数n与公钥的点积不存在

签名文件的验证

验证r和s都是[1,n-1]范围内的整数； 否则，验证失败，计算e = HASH(n)，HAHS()为签名生成过程第1步中使用的哈希函数。 从 e 的最左边 L_n 位开始计算 z。 计算参数w：计算两个参数u1和u2：计算(x1,y1)，如果(x1,y1)不是椭圆曲线上的一个点，则验证失败：如果下面的恒等式不成立，则验​​证失败：

以上就是椭圆曲线数字签名算法（ECDSA）的生成和验证的完整过程。 也可以在wiki_ECDSA中看到上述验证方式正确性的证明过程。 无论使用什么编程语言来实现，数字签名的生成和验证都必须遵循上述理论和步骤。

4. go-ethereum中的椭圆曲线数字签名算法

go语言安装包自带的crypto/ecdsa包中包含了关于椭圆曲线的结构声明和操作函数，以及ECDSA签名生成和校验的完整实现代码。 但是以太坊（go-ethereum）并没有采用这个crypto/ecdsa包来实现自己的数字签名算法。 尽管如此，这部分代码还是有必要阅读的，原因有二：1.其中定义的一些行为接口和结构类型，go-ethereum中的代码仍然使用，方便调用； 2. 它ECDSA的实现代码写的简洁明了，非常适合ECDSA初学者学习。

go语言包中ecdsa代码包

go语言包自带的crypto/ecdsa相关结构如下UML图所示：

与上一章ECDSA的算法理论相比，上面的结构体和接口声明非常容易理解。

的坐标。

.

可以看出，go语言自带的crypto/ecdsa代码包，从结构体的成员到方法的声明，都力图使其所代表的ECDSA算法理论清晰易懂。 关于实现函数，推荐ecdsa/ecdsa.go中的Sign()和Verify()这两个函数

[清楚的]

//go-1.x/src/crypto/ecdsa/ecdsa.go funcSign(randio.Reader,priv*PrivateKey,hash[]byte)(r,s*big.Int,errerror) funcVerify(pub*PublicKey,hash []byte, r, s*big.Int) 布尔

以上两个函数的实现过程严格遵循上一章介绍的算法理论中的签名生成和验证过程。 对于加密算法实现的编码会有一些很好的启发。 有兴趣的朋友可以找源码看看。

在 go-ethereum 中调用 ECDSA

go-ethereum中实际使用的ECDSA函数实现来自于第三方库libsecp256k1，它是一个C++库，已经在比特币代码中使用（github_bitcoin）。 它被认为是一个针对椭圆曲线优化的 secp256k1 实现库。 secp256k1对应一组特定的椭圆曲线数字签名参数，包括曲线方程和签名操作所需的一系列参数等。secp256k1最早应用于比特币，其参数详见secp256k1，详细说明了曲线方程是y^2 = x^3 + 7，其形状如下图所示：

在go-ethereum源码中，/crypto/下的代码包负责所有与加密相关的操作，libsecp256k1库的源码也存放在/secp256k1/的子路径下。 方法被调用。

处理数字签名

以go-ethereum中的交易对象代码为例，ECDSA签名相关的操作都放在一个名为Signer的接口及其实现中。

在接口声明的方法中，Sender()用于从tx对象携带的数字签名中解析出公钥，并转换为Address类型变量； SignatureValues()从tx对象中取出数字签名的R、S、V三部分； hash() 返回当前tx对象需要数字签名的内容，即对tx对象中的一些成员变量进行RLP编码得到Hash值； Equal() 用于比较 Signer 实现主体对象。 可以看出，该接口及其实现主要提供了对生成的数字签名进行操作的方法。

Signer的三个实现类中，HomesteadSigner可以通过持有FrontierSigner对象来保存代码。 关于EIP155：EIP（Ethereum Improvement Proposals，EIP）是对以太坊要求的总结。 EIP155 是比较重要的要求之一。 它增加了一个简单的方法来抵抗重放攻击以太坊计算公式，在对tx进行签名（或恢复签名）时，需要Hash(*Transaction)函数中的RLP编码链接。 多选几个成员变量，所以重新定义了EIP155Signer中的Hash()。

从数字签名中恢复公钥（地址）

从数字签名中恢复（解析）地址变量的函数称为 recoverPlain()：

[清楚的]

//core/types/transaction_signing.go funcrecoverPlain(sighashcommon.Hash,R,S,Vb*big.Int,homesteadbool)(common.Address,error){ V:=byte(Vb.Uint64()-27) 如果！ crypto.ValidateSignatureValues(V,R,S,homestead){ return common.Address{},ErrInvalidSig } //encodesignatureinuncompressedformat r,s:=R.Bytes(),S.Bytes() sig:=make([]byte, 65 ) 复制(sig[32-len(r):32],r) 复制(sig[64-len(s):64],s) sig[64]=V //recoverthepublickeyfromthesignaturepub,err:=crypto.Ecrecover (sighash[:],sig) iferr!=nil||len(pub)==0||pub[0]!=4{ return common.Address{},err } //convertpubKeytoAddress varaddrcommon.Address copy(addr[ : ], crypto.Keccak256(pub[1:])[12:]) return addr, nil }

在上面的recoverPlain()函数体中，

首先调用crypto.ValidateSignatureValues()验证数字签名是否正确有效。 crypto包的这个方法是通过调用libsecp256k1库的API，遵循ECDSA算法理论的数字签名验证部分来完成的；

其次，将R、S、V拼接成需要的数字签名串；

然后调用crypto.Ecrecover()根据数字签名内容sighash和签名串sig恢复数字签名的公钥。 当然，crypto包的方法还是调用libsecp256k1库的API来完成；

最后在返回的公钥中，去掉flag头所在的第一个字节（值为4），生成其SHA-3（256位）哈希值，然后截取其中的后20个字节，即为最终返回的地址类型变量。

生成数字签名

为 tx 对象生成数字签名的函数称为 SignTx()

[清楚的]

//core/types/transaction_signing.go funcSignTx(tx*Transaction,sSigner,prv*ecdsa.PrivateKey)(*Transaction,error){ h:=s.Hash(tx) sig,err:=crypto.Sign(h[ :],prv) iferr!=nil{ returnnil,err } returntx.WithSignature(s,sig) }

从SignTx()函数体可以看出，在Signer.Hash()方法提供了待签名的内容后（即Transaction对象的部分成员经过RLP编码后进行哈希），生成的主要工作是签名交给 crypto.Sign() 函数来完成。 Sign()函数体如下：

[清楚的]

///crypto/signature_cgo.go funcSign(hash[]byte,prv*ecdsa.PrivateKey)(sig[]byte,errerror){ iflen(hash)!=32{ returnnil,fmt.Errorf(...)// hashmustbe32bytes } seckey:=math.PaddedBigBytes(prv.D,n:prv.Params().BitSize/8) deferzeroBytes(seckey) returnssecp256k1.Sign(hash,seckey) }

可以看出，crypto.Sign()函数通过调用libsecp256k1库的API完成了椭圆曲线数字签名的生成。

公钥和地址

以太坊中使用的Address类型地址变量，比如每个账户的地址，来自于椭圆曲线数字签名使用的公钥。 在数字签名中，公钥可以在多个签名中重复使用，体现在以太坊的账户中，即一个账户下的多个交易，即多个不同的交易对象以太坊计算公式，它们所做的数字签名都使用相同的公钥。

具体到变量类型，Address类型是一个长度为20字节的字符串，而椭圆曲线数字签名中公钥的本义应该是曲线上某点的坐标（X，Y），所以必须有格式的相互转换。 在代码中，这涉及到三种不同的格式（类型）： address变量是一个长度为20字节的Address类型的字符串； publicKey 变量是一个长度未知的字符串； 椭圆曲线上的公钥是一个点的坐标，由ecdsa.PublicKey{}中的成员X和Y表示。

publicKey变量转换为Address类型，在前面提到的core.types.recoverPlain()函数体（函数末尾）中引入。

publicKey字符串类型和ecdsa.PublicKey{}类型的格式转换函数由crypto代码包定义。

[清楚的]

//crypto/crypto.go funcToECDSAPub(pub[]byte)*ecdsa.PublicKey{ x,y:=elliptic.Unmarshall(S256(),pub) return&ecdsa.PublicKey{Curve:S256(),X:x,Y: y} } funcFromECDSAPub(pub*ecdsa.PublicKey)[]byte{ returnliptic.Marshall(S256(),pub.X,pub.Y) }

crypto.ToECDSAPub()函数将一个publicKey字符串转换为ecdsa.PublicKey{}类型中点坐标X、Y的形式，FromECDSAPub()函数则进行相反的操作。 调用的elliptic.Unmarshall()函数的逻辑也很简单，就是将[]byte字符串从flag头中去掉后，分为两部分，分别赋值给X和Y，然后从[]byte 到 big.Int ，就是这样。

ps，上面代码中的S256()是本地代码写的转换函数，返回一个elliptic.Curve接口的实现类。 基于secp256k1的椭圆曲线参数，为方便起见，实现了接口声明的所有曲线操作函数。 使用go语言包中的结构体/接口类型来使用secp256k1椭圆曲线。

概括：